UQ of ML
Uncertainty Quantification of ML
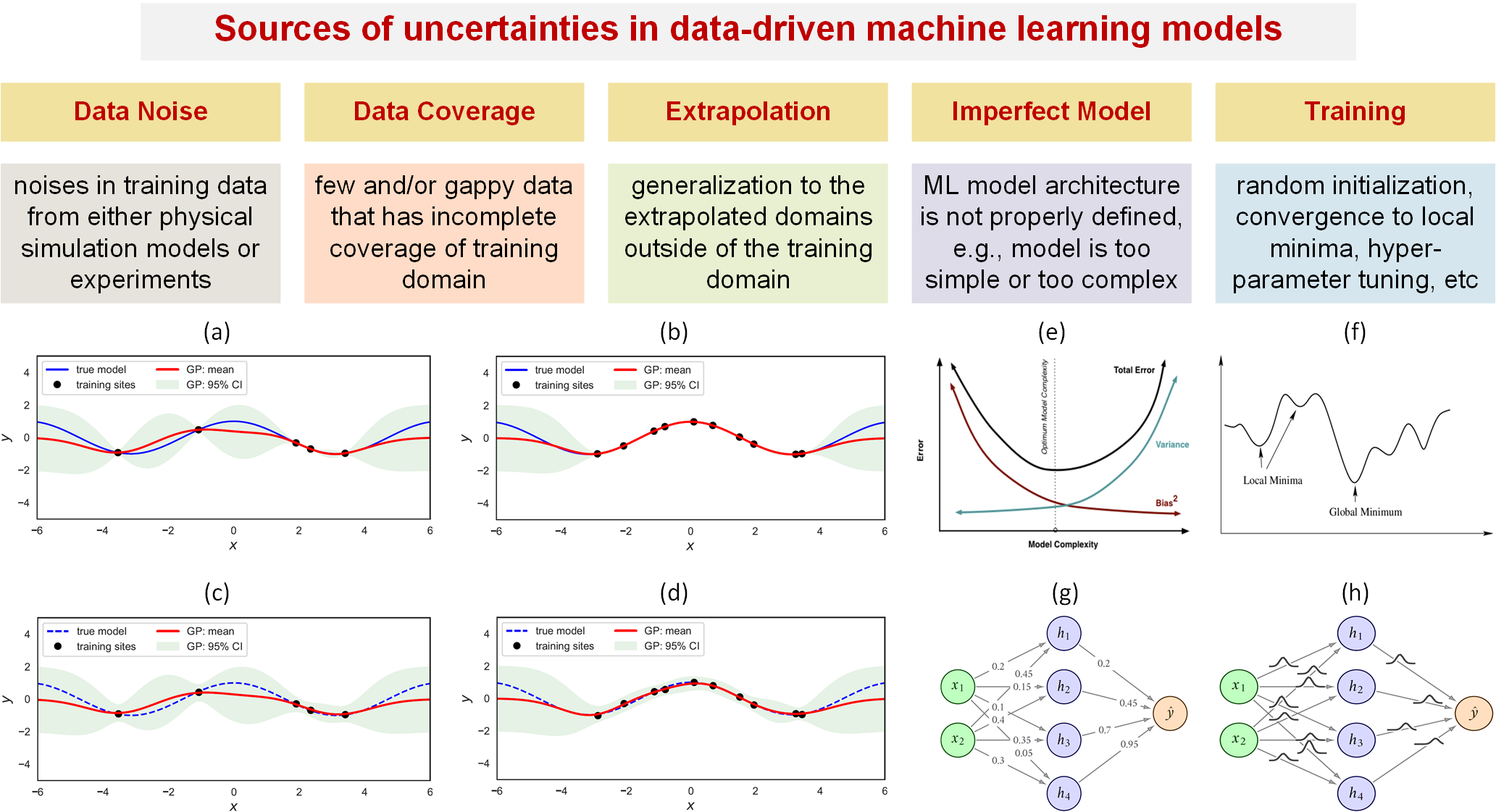
ML-based models are subject to approximation uncertainties when they are used to make predictions. Such uncertainty exists even within the training domain because the training data can be sparse. We summarize the sources of uncertainties for ML models into the following five categories. (1) Data noise – noises in training data from either physical simulation models or experiments can lead to ML uncertainty. (2) Data coverage – few and/or gappy data that has incomplete coverage of the training domain can cause ML uncertainty. (3) Extrapolation – generalization of the ML models to the extrapolated domains outside of the training domain can result in large uncertainties. (4) Imperfect model – when a ML model’s architecture is not properly defined, e.g., the model is too simple or too complex with respect to the data. (5) Training process – issues such as random initialization, convergence to local minima, hyperparameter tuning, posterior inference for Bayesian neural nets, etc. can lead to ML uncertainty. A combination of various sources of uncertainties can greatly affect the accuracy of ML models. Unlike the uncertainty sources in physics-based modeling (data, numerical, model, parameter and code), these sources are usually not well-separated from each other. Ensuring robustness especially in the context of extrapolation is a grand challenge.
Our research on UQ of ML focuses on pursuing new research ideas based on Monte Carlo Dropout (MCD), Deep Ensembles (DE) and Bayesian neural network (BNN) to quantify the prediction uncertainties in deep neural networks (DNNs), as they have the greatest potential for SciML applications in nuclear engineering. We are developing novel approaches that can efficiently implement the variational Bayesian methods for BNN, as well as performing systematic benchmark studies for different UQ methods. We will also focus on developing gradient-based Bayesian inference methods to train BNNs. The Hamiltonian Monte Carlo (HMC) algorithm is a type of MCMC algorithm designed for drawing samples from probability distributions by computing the gradient of the Hamiltonian equations in the direction of high-probability regions, leading to better convergence of MCMC sampling. We will develop efficient HMC-enhanced MCMC exploration of the posterior distributions of BNN parameters, for both steady-state and transient problems in representative nuclear engineering applications.