Hybrid Monte Carlo – FDSA method for k-eigenvalue problem

ARDOR Lab member: Jiahao Chen, Jason Hou
Collaborator: Kostadin Ivanov (NCSU)

he Monte Carlo-Fission Diffusion Synthetic Acceleration (MC-FDSA) method is developed as a hybrid neutronics method for the purposes of acceleration in source convergence and variance reduction in Monte Carlo methods. The low-order diffusion-like FDSA problem is constructed with MC tally results over a spatial mesh and to which the solutions are applied to the high-order MC simulation through neutron weights updating scheme.

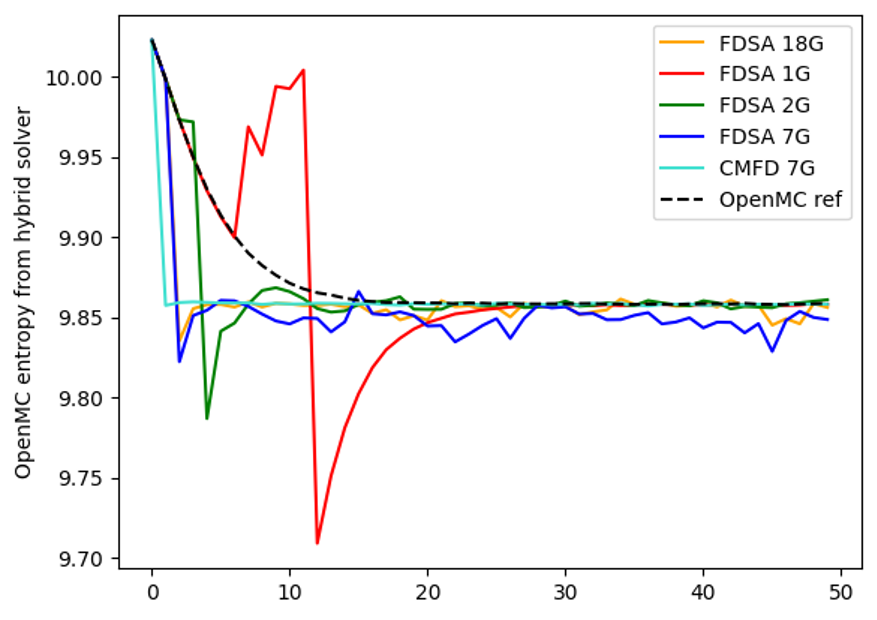
The FDSA method was first implemented and investigated in an SN solver and compared against the coarse mesh finite difference (CMFD) method for acceleration in source convergence, which completed the proof of concept and laid of the foundation for its application in the hybrid neutronic methods for k-eigenvalue problems. Shortly after this, the FDSA method was implemented first in a multigroup MC-FDSA solver and tested with 1D multigroup slab problem. The MC-FDSA method was found to be able to provide a speedup in source convergence by a factor of 8 – 10 in different tests.

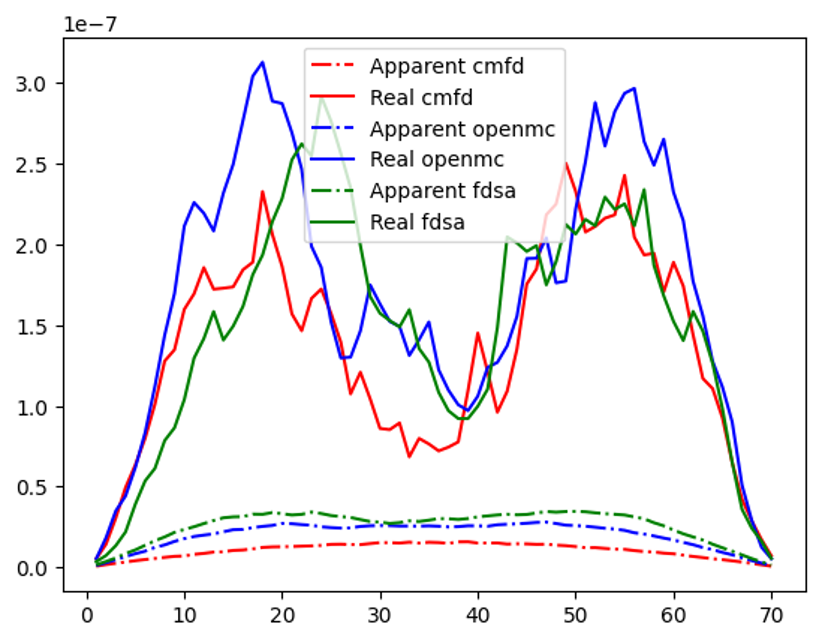
The implementation of MC-FDSA in continuous energy mode is completed with OpenMC and tested with the C5G7 benchmark problem. Results shown that the method provides similar acceleration to that in MC-CMFD and the source convergence is achieved almost instantly with the feedback from FDSA. As for variance reduction in the active cycles, the continuous energy MC-FDSA also shows its capability in reducing the variance by 40% in problems with higher dominance ratio. These results suggest that the MC-FDSA method is an adequate candidate as a hybrid neutronics method for reactor criticality calculations and future improvements could be done on coarse mesh capability and convergence stability studies.